Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
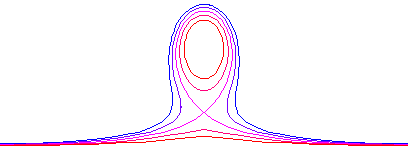
Die Einteilung der Kurven dritten Grades
Einige interessante Kurven
Analogien zwischen Kegelschnitten und Kurven dritten Grades
Der Horopter - eine bemerkenswerte Raumkurve
In der Mathematik sind eine Unmenge von verschiedenen Kurven bekannt. Manche treten in der Praxis auf (z.B. bei der Bewegung von Himmelskörpern oder Maschinenteilen), andere wurden zur Lösung von bestimmten Problemen erfunden. Wir wollen versuchen, ein bisschen Ordnung in diese Fülle zu bringen.Wen die Formeln nicht interessieren, der kann sich einfach an den Bildern freuen :-)
Bekanntlich gehört zu jeder Kurve in einem kartesischen Koordinatensystems eine bestimmte Gleichung. Wir betrachten zunächst einmal nur Kurven in der Ebene. Wenn die Gleichung als Polynom in x und y geschrieben werden kann (z.B. x³ + y³ - 3axy = 0), bezeichnet man die Kurve als algebraische Kurve. Die höchste Potenz von x bzw. y gibt den Grad der Kurve an; er bestimmt auch, wie viele Schnittpunkte sie mit einer Geraden haben kann. Im Beispiel haben wir also eine Kurve dritten Grades; sie kann eine Gerade in maximal drei Punkten schneiden.
Eine lineare Gleichung ergibt einfach eine Gerade. Kurven zweiten Grades sind die Kegelschnitte - hier gibt es drei verschiedene Typen (Ellipse, Parabel, Hyperbel). Bei Kurven dritten Grades (auch kubische Kurven genannt) sind, wie die Überschrift andeutet, schon viel mehr verschiedene Formen möglich. Je höher der Grad der Kurve, um so unübersichtlicher wird die Angelegenheit. Eine Kurve, in deren Gleichung auch transzendente Funktionen vorkommen (z.B. Exponential- oder Winkelfunktionen), heißt transzendente Kurve. Ein Beispiel dafür sind die Zykloiden, aber auch die archimedische und die logarithmische Spirale.
Die Kegelschnitte wurden schon in der Antike ausführlich untersucht. Im 17. Jahrhundert beschäftigten sich die Mathematiker auch mit vielen anderen Kurven und erfanden raffinierte Tricks, um ihre Tangenten zu bestimmen oder den Flächeninhalt zu berechnen. (Daher sind so viele Kurven nach Personen benannt.) Diese Arbeiten waren die Vorbereitung zur Erfindung der Differentialrechnung durch Isaac Newton (1643 - 1727) und Gottfried W. Leibniz (1646 - 1716). Damit stand endlich eine Methode zur Verfügung, mit der man jede beliebige Kurve untersuchen konnte. Newton verwendete sie 1667 dazu, die ebenen Kurven dritten Grades zu klassifizieren. Er stellte fest, dass man immer geeignete Koordinaten einführen kann, so dass die Gleichung in einer dieser vier Formen geschrieben werden kann:
Dabei muss das Koordinatensystem allerdings nicht rechtwinkelig sein. Innerhalb dieser vier Hauptformen fand er 72 Typen von Kurven. Später wurden noch weitere 6 Typen entdeckt. Man kann natürlich darüber streiten, wann zwei Kurven zu verschiedenen Arten gehören. Leonhard Euler (1707 - 1783) teilte in seiner Schrift "Introductio in analysin infinitorum" die Kurven dritten Grades nur nach Anzahl und Typ der Asymptoten ein und kam dabei auf 16 verschiedene Möglichkeiten.
Ich möchte in diesem Artikel die wichtigsten Typen von kubischen Kurven vorstellen. Dabei werde ich mich an Newtons
Einteilung halten, aber in umgekehrter Reihenfolge, weil so die einfacheren Fälle zuerst kommen. Anschließend
werden wir einige spezielle Kurven kennenlernen, die historisch bedeutsam oder sonstwie interessant sind.
Newton entdeckte einige bemerkenswerte Parallelen zwischen Kurven dritten Grades und Kegelschnitten.
Darauf werde ich im dritten Abschnitt eingehen. Schließlich möchte ich noch eine Raumkurve vorstellen,
die mit einigen der erwähnten ebenen Kurven zusammenhängt.
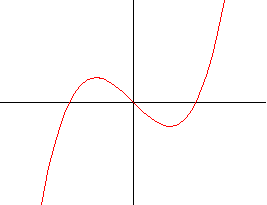 Das ist die aus dem Schulunterricht (Kurvendiskussionen) wohlbekannte kubische Parabel,
der Graph einer Funktion 3. Grades. Sie hat zwei Richtungen ins Unendliche, aber keine geradlinige
Asymptote.
Das ist die aus dem Schulunterricht (Kurvendiskussionen) wohlbekannte kubische Parabel,
der Graph einer Funktion 3. Grades. Sie hat zwei Richtungen ins Unendliche, aber keine geradlinige
Asymptote.
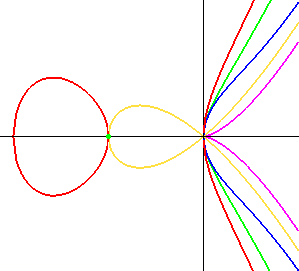 Die Kurven dieses Typs - Newton nannte sie divergierende Parabeln - erhält man
aus dem vorigen, indem man y an allen Stellen, wo es nicht negativ ist, durch ±√y ersetzt.
Dabei entsteht eine zur x-Achse symmetrische Kurve.
Je nachdem, wie die Nullstellen der Funktion verteilt sind, ergibt sich eine zusammenhängende,
glockenförmige Kurve (blau), eine Kurve mit einer Spitze (violett), einer Schlinge (gelb), einem
Oval (rot) oder einem isolierten Punkt (grün).
Die Kurven dieses Typs - Newton nannte sie divergierende Parabeln - erhält man
aus dem vorigen, indem man y an allen Stellen, wo es nicht negativ ist, durch ±√y ersetzt.
Dabei entsteht eine zur x-Achse symmetrische Kurve.
Je nachdem, wie die Nullstellen der Funktion verteilt sind, ergibt sich eine zusammenhängende,
glockenförmige Kurve (blau), eine Kurve mit einer Spitze (violett), einer Schlinge (gelb), einem
Oval (rot) oder einem isolierten Punkt (grün).
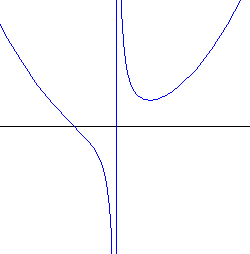 Diese Kurve heißt auch Newtonscher Dreizack (Trident). Man kann die Gleichung
umformen zu
Diese Kurve heißt auch Newtonscher Dreizack (Trident). Man kann die Gleichung
umformen zu
y = ax² + bx + c + d/x
Man sieht, dass die Kurve die y-Achse als senkrechte Asymptote hat und sich außerdem asymptotisch an die Parabel y = ax² + bx + c annähert.
Dieser Typ enthält die meisten verschiedenen Formen. Für e = 0 ist die Kurve symmetrisch zur x-Achse - das ist bei allen folgenden Beispielen der Fall.
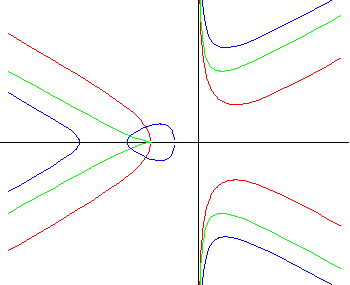
Die Kurve hat drei Äste und drei gerade Asymptoten, also mehr als eine normale Hyperbel. Newton bezeichnet sie daher als redundante (überzählige) Hyperbel. Auch hier können Spitzen, Schlingen, Ovale oder isolierte Punkte auftreten.
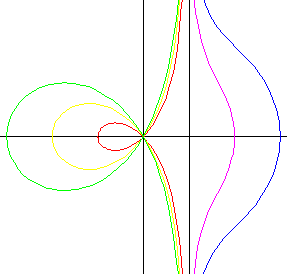
Die defiziente (mangelhafte) Hyperbel hat nur eine gerade Asymptote.
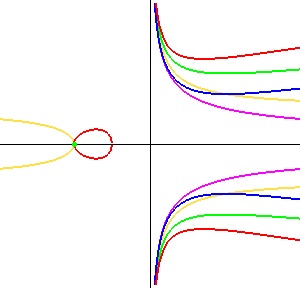
In diesem Fall hat die Kurve eine gerade Asymptote und eine Parabel, der sie sich asymptotisch annähert. Sie wird daher als parabolische Hyperbel bezeichnet. Die Parabel kann auch zu zwei parallelen Geraden (gelb, für b = 0 und c > 0) oder einer Geraden (violett, für b = c = 0) werden. Ist b = 0 und c < 0, verschwindet sie ganz, und die Kurve hat nur eine Asymptote (nicht im Bild).