Die Zykloide und verwandte Kurven

Eine Zykloide ist "nichts anderes als der Weg, den ein Nagel eines Rades in der Luft zurücklegt, wenn dieses seine übliche Bewegung ausführt" (Pascal). Diese Kurve (auch Trochoide genannt) und ihre Verwandten, die Epizykloiden und Hypozykloiden, sehen hübsch aus und haben sehr interessante Eigenschaften. Es handelt sich um transzendente Kurven, das heißt, sie können nicht durch eine algebraische Gleichung beschrieben werden. Die Zykloide wurde im 17. Jahrhundert ausgiebig studiert und hat wesentlich zur Entwicklung der Differential- und Integralrechnung beigetragen.

Die Zykloide
Epizykloiden
Hypozykloiden
Die Zykloide in Geschichte, Technik und Literatur
Spirograph
Exkurs: Kurven in Parameterdarstellung
Literatur und Links

Die Zykloide

Bild: mathworld.wolfram.com

Die Zykloide ist die Kurve, die ein Punkt auf dem Umfang eines Kreises beschreibt, wenn der Kreis längs einer Geraden abrollt.

Der Punkt P soll am Anfang der Bewegung die Gerade berühren. Dann erhält man die Gleichungen:

x = a(t - sin t)
y = a(1 - cos t)

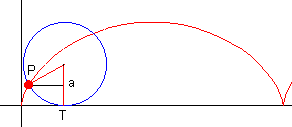
a ist dabei der Radius des Kreises, t der Winkel, um den er sich bereits gedreht hat. (Zur Parameterdarstellung von Kurven siehe den Exkurs, der aber auch übersprungen werden kann.) Ein Applet dazu gibt es auf http://www.ies.co.jp/math/products/calc/applets/cycloid/cycloid.html.

Wenn man statt des Punktes P den gegenüberliegenden Punkt betrachtet, erhält man die alternativen Gleichungen

x = a(t + sin t)
y = a(1 + cos t)

Die Fläche unter einem Kurvenbogen kann man durch Integrieren berechnen:

Das ist das Dreifache der Fläche des erzeugenden Kreises.

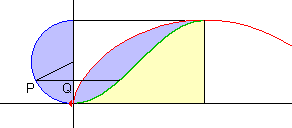
Dieses Ergebnis erhielt Roberval (1602 - 1675) ohne Integralrechnung, indem er die Bewegung des Punktes P in zwei Bewegungen zerlegte: die Drehung von P um den Kreismittelpunkt und die Bewegung von Q, der Projektion von P auf den senkrechten Kreisdurchmesser. Bei einer halben Umdrehung des Rades beschreibt der Punkt P einen Halbkreis mit der Fläche aČp/2, der Punkt Q eine Sinuskurve. Die Fläche unter dieser Kurve ist aus Symmetriegründen halb so groß wie das umschriebene Rechteck, also 2a·ap/2 = aČp.
Jetzt zerlegt Roberval in Gedanken die Halbkreisfläche in schmale, horizontale Streifen (Indivisiblen), die er nach rechts bis zur Sinuskurve verschiebt. (Die beiden blauen Flächen sind also gleich groß.) Die gesamte Fläche unter der Zykloide beträgt daher A = 3aČp/2.
(Die Indivisiblenmethode, die hier verwendet wird, ist allerdings eine Vorläuferin der Integralrechnung. Sie stammt von Cavalieri, wurde aber auch von Roberval selbständig entdeckt.)

Die Länge eines Kurvenbogens beträgt

s = 8a.

Der Schwerpunkt des Flächenstücks hat die Koordinaten S(ap / 5a/6).

Der Tangentialvektor im Punkt P hat die Koordinaten 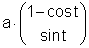und steht daher normal auf den Vektor TP, der den Berührpunkt des Kreises mit dem Kurvenpunkt verbindet. Daraus ergibt sich eine sehr einfache Tangentenkonstruktion.

Der Radius des Krümmungskreises beträgt 2aÖ2·Ö(1 - cos t) = 4a·sin(t/2). Das ist das Doppelte der Strecke TP.

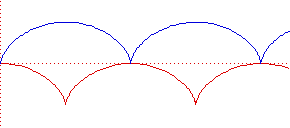
Die Evolute der Zykloide hat die Gleichung

x = a(t + sin t)
y = a(-1 + cos t)

Das entspricht genau der alternativen Gleichung, wobei die Kurve um 2a nach unten verschoben wurde. Die Evolute der Zykloide ist daher wieder eine (kongruente) Zykloide.

Wenn der Punkt P im Inneren des erzeugenden Kreises liegt, entsteht eine verkürzte Zykloide; liegt er außerhalb, so erhält man eine verlängerte Zykloide mit Schleifen. Alle diese Kurven fasst man auch unter der Bezeichnung Trochoiden (Radkurven) zusammen. Die allgemeine Gleichung lautet, wobei b der Abstand von P zum Kreismittelpunkt ist:

x = at - b sin t
y = a - b cos t

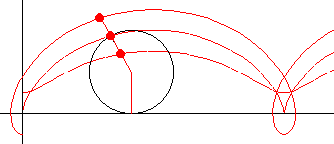
Man kann eine Zykloide auch definieren als Zusammensetzung einer Translation (geradlinigen Verschiebung) und einer Rotation. Eine einfache Zykloide erhält man genau dann, wenn die Geschwindigkeit der Translation und die Tangentialgeschwindigkeit bei der Rotation gleich groß sind.

Siehe auch: MacTutor, Famous Curves Index - mathworld.wolfram.com - Xah Lee

↑ nach oben - weiter