Hypozykloiden

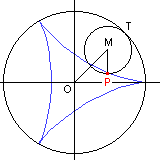
Eine Hypozykloide erhalten wir, wenn der kleine Kreis innen am großen abrollt. Sie hat die Gleichung:

x = (b - a)cos t + a cos(1 - b/a)t
y = (b - a)sin t + a sin(1 - b/a)t

Auch hier erhalten wir nach einer Umdrehung eine geschlossene Kurve, wenn b/a eine ganze Zahl ist. Diesmal setzen wir m = b/a - 1. Dann vereinfacht sich die Gleichung zu

x = ma cos t + a cos mt
y = ma sin t - a sin mt

In der alternativen Form lautet sie:

x = ma cos t - a cos mt
y = ma sin t + a sin mt

Für Länge und Flächeninhalt der Hypozykloide gelten die Formeln

s = 8ma
A = m(m - 1)aČp

Die Tangente erhält man genauso wie bei Zykloide und Epizykloide. Die Gleichung der Evolute lautet:

x = (ma cos t - a cos mt)
y = (ma sin t + a sin mt)

Die Evolute ist also eine um den Faktor 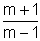vergrößerte, gedrehte Kopie der ursprünglichen Hypozykloide.

Eine Hypozykloide ensteht auch durch die Zusammensetzung von zwei Rotationen im zueinander entgegengesetzten Drehsinn.

Siehe dazu: MacTutor, Famous Curves Index - Xah Lee

Spezielle Hypozykloiden

Ist b = 2a (m = 1), so wird aus der Kurve eine Strecke (der Durchmesser des großen Kreises).

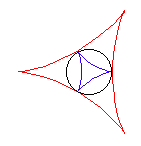
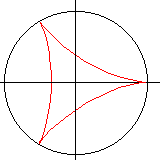Für b = 3a (m = 2) erhält man eine Tricuspoide (Dreispitzkurve).
(Sie ist auch unter der englischen Bezeichnung "deltoid" bekannt, aber im Deutschen ist ein Deltoid ein Drachenviereck.) Ihre Maße sind

l = 16a, A = 2aČp

Siehe dazu: MacTutor, Famous Curves Index - Xah Lee

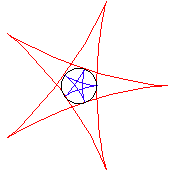
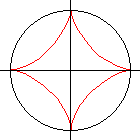Für b = 4a (m = 3) ergibt sich eine Astroide (Sternkurve) mit den Maßen

l = 24a, A = 6aČp

Diese Kurve kann man auch erhalten, indem man die Endpunkte einer Strecke von konstanter Länge b die Koordinatenachsen entlanggleiten lässt. In kartesischen Koordinaten lautet ihre Gleichung:

x^2/3 + y^2/3 = b^2/3

Siehe dazu: MacTutor, Famous Curves Index - Xah Lee

zurück - ↑ nach oben - weiter