Epizykloiden

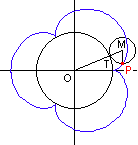
Wenn ein Kreis vom Radius a außen auf einem Kreis vom Radius b abrollt, beschreibt ein Punkt auf dem Kreisumfang eine Epizykloide. Ihre Gleichung lautet:

x = (a + b)cos t - a cos(1 + b/a)t
y = (a + b)sin t - a sin(1 + b/a)t

Wenn b/a eine ganze Zahl ist, erhalten wir nach einer Umdrehung eine geschlossene Kurve. Wir setzen m = 1 + b/a = OM/a. Dann können wir die Gleichung einfacher schreiben:

x = ma cos t - a cos mt
y = ma sin t - a sin mt

Wie bei der Zykloide, können wir auch hier den Punkt betrachten, der P gegenüberliegt, und die Gleichung in einer alternativen Form angeben:

x = ma cos t + a cos mt
y = ma sin t + a sin mt

Für die Länge der Epizykloide und den Inhalt der umschlossenen Fläche erhalten wir die Formeln

s = 8ma
A = m(m + 1)a²p

Der Tangentialvektor steht auch hier normal auf den Vektor TP. Die Evolute hat die Gleichung

x = (ma cos t + a cos mt)
y = (ma sin t + a sin mt)

Das ist die Gleichung der Epizykloide in der alternativen Form, um der Faktor 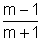verkleinert. Die Evolute ist also eine verkleinerte, gedrehte Kopie der ursprünglichen Kurve.

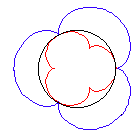
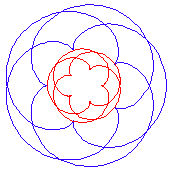
(Wenn das Verhältnis b/a eine rationale Zahl ist, schließt sich die Kurve erst nach mehreren Umdrehungen. Ist es irrational, schließt sie sich nie.)

Eine Epizykloide ensteht auch durch die Zusammensetzung von zwei Rotationen, die im selben Drehsinn erfolgen.

Siehe dazu: MacTutor, Famous Curves Index - Xah Lee

Spezielle Epizykloiden

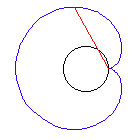Für b = a (m = 2) ergibt sich eine Kardioide (Herzkurve). Für Umfang und Fläche erhält man:

s = 16a, A = 6a²p

Diese Kurve kann man auch anders erhalten, und zwar als Kreiskonchoide (Pascal'sche Schnecke): Man zeichnet von einem Punkt auf dem Kreisumfang eine Sehne und verlängert sie um den Kreisdurchmesser. Wenn die Sehne sich dreht, beschreibt der Endpunkt der Verlängerung eine Kardioide.

Wenn die Spitze der Kardioide im Koordinatenursprung liegt, lautet die Gleichung in Polar- bzw. kartesischen Koordinaten:

r = 2a(1 - cos j)
(x² + y² + 2ax)² = 4a²(x² + y²)

Siehe dazu: MacTutor, Famous Curves Index - Xah Lee

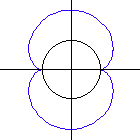Ist b = 2a (m = 3), so erhält man eine Nephroide (Nierenkurve). Sie hat die Maße

s = 24a = 12b
A = 12a²p = 3b²p

Siehe dazu: MacTutor, Famous Curves Index - Xah Lee

zurück - ↑ nach oben - weiter