Verallgemeinerung: Cassinische Ovale

Wir wollen jetzt für das Produkt der Abstände auch andere Werte zulassen, es soll also gelten: PF₁·PF₂ = c². Dabei ergeben sich ganz verschiedene Kurven, je nachdem, wie groß wir c wählen. Man nennt sie Cassinische Kurven - Näheres dazu siehe unten. Die Gleichungen erhält man wie vorhin:

(1a)     (x² + y²)² - 2a²(x² - y²) = c⁴ - a⁴

(2a)     r⁴ - 2a²r²cos(2φ) = c⁴ - a⁴

Wenn wir y = 0 setzen, erhalten wir: x² = a² + c² oder x² = a² - c². Der erste Wert ist auf jeden Fall positiv, der zweite nur, wenn c < a. In diesem Fall gibt es also vier Schnittpunkte mit der x-Achse, und die Kurve zerfällt in zwei Teile.

x = 0 ergibt: y² = -a² + c² oder y² = -a² - c². Die zweite Lösung ist auf jeden Fall negativ, die erste ist nur dann positiv, wenn c > a. In diesem Fall schneidet die Kurve also die y-Achse in zwei Punkten.

Schließlich untersuchen wir noch die Extrempunkte. Aus ∂F/∂x = 0 folgt: x = 0 oder r = a. Die Extrempunkte liegen also auf der y-Achse oder auf dem Kreis durch die Pole (blau). Falls -a² + c² = a², also c² = 2a², fallen je drei Extrempunkte zusammen, und die Kurve hat dort einen Flachpunkt. (Die Wendepunkte, falls vorhanden, liegen auf einer um 90° gedrehten Lemniskate - grün.)

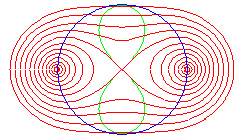
Wir müssen also fünf Fälle unterscheiden:

c < a: Zwei Eier

Die Kurve zerfällt in zwei eiförmige Teile. Sie schneidet die x-Achse in den Punkten (±√(a²+c²)/0) und (±√(a²-c²)/0), auf der y-Achse gibt es keine Kurvenpunkte. Wenn man die Polargleichung (2a) nach r² auflöst, erhält man zwei, eine oder gar keine Lösung, je nachdem ob sin(2φ) kleiner, gleich oder größer als c²/a² ist. Ein Strahl, der vom Ursprung ausgeht, kann mit der Kurve also zwei Schnittpunkte haben. Aus dem Satz von Vieta ergibt sich in diesem Fall: r₁²· r₁² = a⁴ - c⁴; das Produkt der beiden Radien ist also konstant. Wenn man die Kurve daher an einem Kreis mit dem Radius ⁴√(a⁴ - c⁴) invertiert, geht sie in sich selbst über. Eine solche Kurve nennt man anallagmatisch.

c = a: Bernoullische Lemniskate

Das ist die Kurve, die wir vorhin untersucht haben. Bernoulli merkte nicht, dass "seine" Lemniskate ein Sonderfall der Ovale war, die Cassini schon 1680, also 14 Jahre vorher entdeckt hatte.

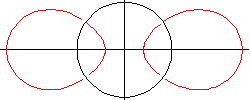
a < c < a√2: Hantel

Die Kurve schneidet die x-Achse in den Punkten (±√(a²+c²)/0) und die y-Achse in (0/±√(c²-a²)). Die obere Hälfte hat zwei Hochpunkte bei r = a und dazwischen einen Tiefpunkt auf der y-Achse; bei der unteren Hälfte ist es natürlich umgekehrt. Wir erhalten daher ein Oval mit einer Einbuchtung in der Mitte, eine Art Hantel oder Bohne. Die Gleichung (2a) hat immer zwei Lösungen für r², von denen aber nur eine positiv, ist. Jeder vom Ursprung ausgehende Strahl schneidet also die Kurve einmal. Man kann zeigen, dass immer gilt: r(φ)²·r(π/2-φ)² = c⁴ - a⁴; die Kurve geht also bei Inversion an einem Kreis mit dem Radius ⁴√(c⁴ - a⁴) in eine um 90° gedrehte Kopie über.

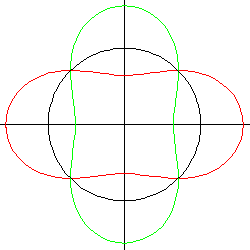
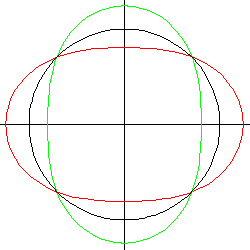
c = a√2: flaches Oval

Der Kreis mit dem Radius a berührt die Kurve in (0/±a). In diesen Punkten fallen also je drei Extrempunkte zusammen, und die Kurve hat dort Flachpunkte (d.h. die Krümmung beträgt an dieser Stelle 0). (Das ist die größte Kurve im Bild ganz oben auf der Seite.)

c > a√2: "Fast-Ellipse"

Wenn c noch größer wird, werden die Ovale immer ellipsenähnlicher. Auch hier erhält man bei Inversion an einem passenden Kreis eine um 90° gedrehte Kurve.

Der französische Astronom Jean-Dominique Cassini (1625-1712) war der Meinung, dass die Bahn der Sonne um die Erde (!) diese Form hat - im Gegensatz zu Johannes Kepler (1571 - 1630), der schon Anfang des 17. Jahrhunderts behauptet hatte, dass die Planeten sich auf Ellipsen um die Sonne bewegen. Nun, ob man die Sonne oder die Erde als Zentrum betrachten, ist nur eine Frage des Gesichtspunkts und für die mathematische Beschreibung egal. Und weil die Erdbahn fast kreisförmig ist, ist es sehr schwer zu unterscheiden, ob es sich um eine Ellipse oder um ein Cassinisches Oval handelt. Erst Isaac Newton (1643 - 1727) konnte aus dem von ihm entdeckten Gravitationsgesetz ableiten, dass die Planetenbahnen Ellipsen sein müssen ("Principia mathematica", erschienen 1687).

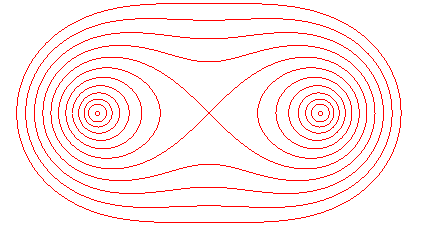
Physikalische Interpretation

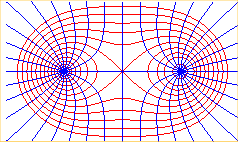
Angenommen, zwei parallele Drähte (normal zur Bildebene) werden gleich aufgeladen (also beide positiv oder beide negativ). Dann bildet sich ein elektrostatisches Feld. Die Energie, die ein geladenes Teilchen in diesem Feld besitzt, bezeichnet man als Potential. Die Äquipotentiallinien dieses Feldes (also die Linien mit konstantem Potential) sind Cassinische Ovale (rote Linien). (Begründung: die elektrostatische Kraft ist proportional zu 1/r, und das Potential ist das Integral davon, also ln(r). Das Gesamtpotential in Bezug auf beide Leiter ist konstant, wenn ln(r₁) + ln(r₂) konstant ist, also auch r₁·r₂.) Die Feldlinien, also die Linien, in deren Richtung die Kraft wirkt, stehen immer normal zu den Äquipotentiallinien (blaue Linien); es sind gleichseitige Hyperbeln. Man erhält sie als Schnittpunkte von zwei Strahlen, die gleich schnell, aber in entgegengesetzter Richtung um zwei feste Punkte rotieren.

Wenn die Drähte in gleicher Richtung von Strom durchflossen werden, entsteht ein Magnetfeld. Die Cassinischen Ovale sind dann die Feldlinien.

Zurück: Die Bernoullische Lemniskate - Weiter: Schleifenkurven im Raum

Zum Inhaltsverzeichnis