Schleife mit Variationen

Die Bernoullische Lemniskate
Verallgemeinerung: Cassinische Ovale
Schleifenkurven im Raum

Bekanntlich besteht die Ellipse aus allen Punkten, für die die Abstandssumme von zwei festen Punkten, den Brennpunkten, konstant ist. Bei der Hyperbel ist die Abstandsdifferenz konstant. Wenn das Verhältnis, also der Quotient der Abstände konstant sein soll, ergibt sich sogar eine noch einfachere Kurve, nämlich ein Kreis (der sogenannte Apollonius-Kreis). Und was ist, wenn man fordert, dass das Produkt der Abstände konstant ist? Dann erhält man eine Kurve 4. Grades.

Die Bernoullische Lemniskate

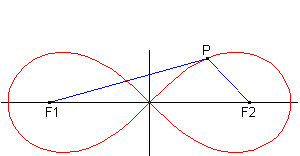
Wir betrachten zuerst den Fall, dass die Pole die Koordinaten F₁(-a/0) und F₂(a/0) haben und für einen Punkt P auf der Kurve gilt: PF₁·PF₂ = a². Diese Kurve wurde von Jakob Bernoulli (1654 - 1705) untersucht. Er nannte sie nach ihrer Form Lemniskate (Schleifenkurve, von griech. lemniskos: Band, Schleife).

In Koordinatenform angeschrieben lautet die Konstruktionsvorschrift:

[(x + a)² + y²][(x - a)² + y²] = a⁴

Das kann man umformen zu

(1)     (x² + y²)² = 2a²(x² - y²)

Man sieht sofort, dass die Kurve zur x- und y-Achse symmetrisch ist. Die Schnittpunkte mit der x-Achse finden wir, indem wir y = 0 setzen. Wir erhalten (a√2/0), (-a√2/0) und (0/0). Der letzte Punkt ist eine Doppellösung und zugleich der einzige Kurvenpunkt auf der y-Achse. Die Kurve hat hier einen sogenannten Doppelpunkt, d.h. sie schneidet sich selbst.

Weil x² + y² = r² und x² - y² = r²(cos²(φ) - sin²(φ)) = r²cos(2φ), lautet die Gleichung in Polarkoordinaten

(2)     r² = 2a²cos(2φ)

Man darf hier durch r² kürzen, weil der Punkt (0/0) sowieso auf der Kurve liegt. r nimmt nur dann reelle Werte an, wenn φ zwischen -45° und 45° oder zwischen 135° und 225° liegt. Die Tangenten in (0/0) haben daher die Steigung ±1.

Die Hoch- und Tiefpunkte einer Kurve, die in der Form F(x,y) = 0 gegeben ist, erhält man, indem man die partielle Ableitung ∂F/∂x = 0 setzt. Das ergibt hier: 4x(x² + y² - a²) = 0, also x = 0 oder x² + y² - a² = 0. Die erste Lösung fällt weg, weil hier auch ∂F/∂y = 0 ist (das ergibt wieder den Doppelpunkt); die zweite ist gleichbedeutend mit r = a. In (2) eingesetzt, ergibt das φ = 30°, und mit den dazu symmetrischen Punkten erhalten wir die Extrempunkte (±a√3/2 / ±a/2).

Eine Parameterdarstellung der Kurve lautet

x² = 2a²t(1 + t)
y² = 2a²t(1 - t)

Dabei ist t = cos(2φ) = r²/2a². Zu jedem Wert von t gehören vier Punkte - wenn t das Intervall [0, 1] durchläuft, erhält man also die ganze Lemniskate.

Den Flächeninhalt der umschlossenen Fläche berechnet man am besten in Polarkoordinaten:

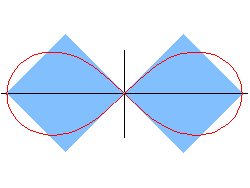
Wenn man die Bogenlänge berechnen will, kommt man auf das elliptische Integral 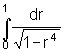, das man nur numerisch berechnen kann. Eine sehr effiziente Berechungsmethode benutzt das arithmetisch-geometrische Mittel: es ist nämlich 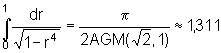. Das Doppelte dieser Zahl, die sogenannte Lemniskatische Konstante, spielt für die Lemniskate die gleiche Rolle wie π für den Kreis (der Umfang der Lemniskate beträgt ca. das 2,622-fache des längsten Durchmessers). Gauß führte dafür die Bezeichnung ϖ (kalligraphisches Pi) ein.

Die Normale auf die Kurve schließt mit dem Radius im Kurvenpunkt den Winkel 2φ (und daher mit der x-Achse 3φ) ein. So kann man die Tangente konstruieren.

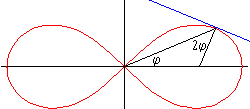
Die Krümmung der Kurve beträgt in der oben angegebenen Parameterdarstellung κ = -3/a·√(t/2).

Man kann die Lemniskate auch auf mechanischem Weg mit Hilfe eines Gelenkvierecks erhalten (Bild): Es ist AB = CD = 2a, AD = BC = a√2. Die Punkte C und D sind fest. Wenn sich die Seiten AD und BC drehen, beschreibt der Mittelpunkt M der Seite AB eine Lemniskate. (Animation dazu)

Auch bei anderen Seitenlängen erhält man ähnliche Schleifenkurven. Der mittlere Teil einer solchen Kurve ist fast gerade. Daher benutzte James Watt (1736 - 1819) bei seiner Dampfmaschine ein solches Gestänge, um eine Drehung in eine geradlinige Bewegung zu verwandeln. Noch heute wird es in manchen PKWs bei der Aufhängung der Hinterachse eingesetzt, damit die Achse beim Federn nur auf und ab, aber nicht seitwärts schwingt¹.

Die Inversion am Kreis ist eine Abbildung, die sozusagen das Innere eines Kreises nach außen kehrt. Man nennt sie auch manchmal "Kreisspiegelung", obwohl sie mit einer physikalischen Spiegelung nichts zu tun hat: Jedem Punkt P wird auf dem Strahl MP ein Punkt P' zugeordnet, so dass MP·MP' = R². Geraden und Kreise gehen dabei wieder in Geraden und Kreise über, und Winkel bleiben gleich groß. Wenn man die Lemniskate an einem Kreis mit Mittelpunkt im Ursprung spiegelt, erhält man eine gleichseitige Hyperbel:

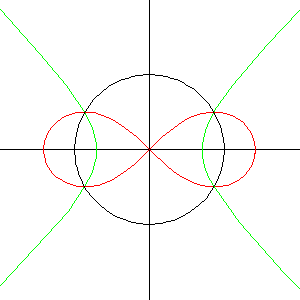
In der komplexen Zahlenebene erhält man die Lemniskate als Bild des Kreises |z - 1| = 1 unter der Abbildung f(z) = √z (im Komplexen gibt es immer zwei mögliche Werte für die Quadratwurzel).

Andere Bedeutungen:

In der Mathematik ist die Lemniskate das Zeichen für "unendlich". Wahrscheinlich leitet sie sich von einer Variante des römischen Zahlzeichens für 1000 (M) ab. In ihrer heutigen Bedeutung wurde sie von John Wallis (1616 - 1703) eingeführt².

In der Esoterik ist sie das Symbol der Vollendung, des ewigen Auf und Ab³. Auch auf zwei Tarotkarten ("Der Magier" und "Die Kraft") ist eine Lemniskate abgebildet. Hier wird sie interpretiert als Sinnbild des ständigen Austauschs zwischen zwei Welten (Makrokosmos und Mikrokosmos). (Allerdings tragen diese Personen auf älteren Darstellungen einfach Hüte mit breiten, geschwungenen Krempen.) In der Symbolik der Freimaurer ist sie ein Zeichen für die weltweite Bruderkette⁴.

1: http://de.wikipedia.org/wiki/Wattgest%C3%A4nge
2: http://jeff560.tripod.com/calculus.html
3: http://www.seelenbilder.net/symbol.htm#Lemniskate
4: http://de.wikipedia.org/wiki/Lemniskate

Weiter: Cassinische Ovale

Zum Inhaltsverzeichnis