Schleifenkurven im Raum

Man kann die Cassinischen Ovale auch als ebene Schnitte eines Torus erhalten. Ein Torus sieht aus wie ein Donut oder Autoreifen. Er entsteht, wenn ein Kreis mit Radius r um eine Achse rotiert, die in der selben Ebene wie der Kreis liegt, wobei der Kreismittelpunkt seinerseits einen Kreis vom Radius R beschreibt.

Nicht jeder Schnitt eines Torus mit einer Ebene ergibt ein Cassinisches Oval (im Allgemeinen erhält man eine "Spirische Kurve"), sondern die Schnittebene muss parallel zur Torusachse sein und von ihr den Abstand r haben. Je nach dem Verhältnis von r und R ergeben sich die verschiedenen Formen der Kurve. Dabei ist a = R und c² = 2Rr. (Die "richtigen" Ovale erhält man, wenn r > R ist. Dann wird der Torus zu einem "Spindeltorus" - er hat kein Loch in der Mitte, sondern durchdringt sich selbst.)

Eine andere interessante Raumkurve, die auch mit den Cassinischen Kurven zusammenhängt, ist das Vivianische Fenster. Es entsteht, wenn man eine Kugel vom Radius R und einen Zylinder mit halb so großem Radius schneidet:

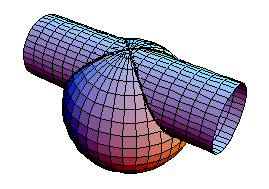
Es wurde vom italienischen Architekten Vincenzo Viviani (1622-1703) untersucht. Wenn man aus einer Halbkugel das Innere des Zylinders entfernt, beträgt die restliche Oberfläche 4R² und das Volumen 8R³/9. Die Kreiszahl π kommt dabei nicht mehr vor! (Beweis - hier wurde eine ganze Kugel mit zwei zylindrischen Löchern betrachtet.) Auf mathcurve.com findet man noch einige andere Möglichkeiten, diese Kurve zu erzeugen.

Wenn man die Vivianische Kurve stereographisch aus dem Südpol auf die äquatorebene projiziert, erhält man eine Bernoullische Lemniskate (rot):

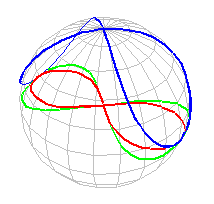
(Zur stereographischen Projektion siehe Mathe-Newsletter 11, Die Geometrie des stumpfen Winkels.) Die Normalprojektion auf dieselbe Ebene ist eine Geronosche Lemniskate (grün) mit der Gleichung x⁴ = R²(x² - y²) bzw. x = R·sin(t), y = R·sin(t)·cos(t). Die von ihr eingeschlossene Fläche ist 4/3 mal so groß wie die der Bernoullischen Lemniskate.

Die stereographische Projektion aus dem Nordpol ergibt übrigens eine gleichseitige Hyperbel. Wenn man einen Scheitel der Kurve als Projektionszentrum wählt, erhält man eine Strophoide.

Wenn man den Radius r des Zylinders verändert, wobei der Zylindermantel weiter durch den Mittelpunkt der Kugel geht, , und die Schnittkurven wider stereographisch projiziert, erhält man die anderen Formen der Cassinischen Ovale. Dabei ist a² = R/(1+2r), c² = 2Rr/(1+2r).

Links:

Unterrichtsprojekt "Kurven": http://haftendorn.uni-lueneburg.de/u1/gym03/expo/jonatur/wissen/mathe/kurven/cassini.htm

mathcurve.com (französisch, mit vielen Animationen):
Lemniskate: http://www.mathcurve.com/courbes2d/lemniscate/lemniscate.shtml
Cassinische Ovale: http://www.mathcurve.com/courbes2d/cassini/cassini.shtml
Vivianisches Fenster: http://www.mathcurve.com/courbes3d/viviani/viviani.shtml

Xah Lee, Visual Dictionary Of Special Plane Curves (englisch):
Lemniskate: http://xahlee.org/SpecialPlaneCurves_dir/LemniscateOfBernoulli_dir/lemniscateOfBernoulli.html
Cassinische Ovale: http://xahlee.org/SpecialPlaneCurves_dir/CassinianOval_dir/cassinianOval.html

Zurück: Cassinische Ovale

Zum Inhaltsverzeichnis