Home

Ich über mich

Texte

Religion

Mathematik

Spiele

Gästebuch

Der Goldene Schnitt

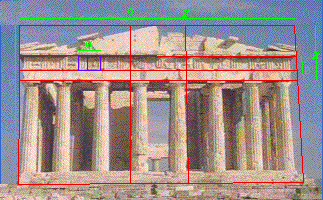
Seit der Antike haben sich Künstler und Architekten gefragt, welche Proportionen als schön empfunden werden. Besonders ästhetisch fand man ein Rechteck, bei dem sich die kürzere Seite zur längeren so verhält wie die längere zur Summe der beiden Seiten – das "Goldene Rechteck". Dieses Seitenverhältnis nannte man "Goldenes Verhältnis" (ratio aurea) oder "Goldenen Schnitt" (sectio aurea):

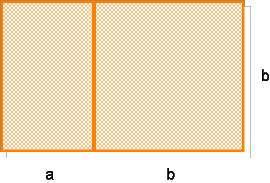
a:b = b:(a+b)

das heißt, wenn man an die längere Seite ein Quadrat anfügt, erhält man wieder ein (größeres) goldenes Rechteck. (Umgekehrt erhält man, wenn man ein Quadrat entfernt, ein kleineres goldenes Rechteck. Diesen Vorgang kann man beliebig oft fortsetzen und bekommt so unendlich viele goldene Rechtecke!)

Auch beim regelmäßigen Fünfeck taucht der Goldene Schnitt auf, und zwar als Verhältnis von Seite und Diagonale:

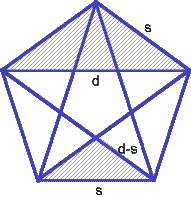
Die beiden schraffierten Dreiecke sind ähnlich, daher gilt: (d-s):s=s:d

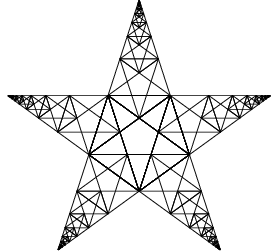
d-s bildet die Seite eines neuen Fünfecks, und so kann man immer kleinere Fünfecke einzeichnen – theoretisch könnte man unendlich lange so weitermachen... Das bedeutet, dass das Verhältnis d:s nicht durch ganze Zahlen ausgedrückt werden kann (denn wenn man ganze Zahlen voneinander subtrahiert, erhält man irgendwann 0). d/s ist also keine rationale Zahl.

Wie berechnet man nun das Verhältnis?

Setzen wir die kürzere Seite gleich 1 und die längere gleich x, so erhalten wir die Gleichung

1:x = x:(x + 1) Þ x² - x - 1 = 0

Die Lösungsformel für quadratische Gleichungen ergibt

Die positive Lösung bezeichnet man meist mit j , sie beträgt » 1,618.

Der Betrag der negativen Lösung ist » 0,618 = j - 1 = 1/j .

Man kann j auch als Kettenbruch darstellen:

Bricht man diesen Kettenbruch irgendwo ab, so erhält man als Näherungswert einen Bruch, dessen Zähler und Nenner aufeinanderfolgende Fibonacci-Zahlen sind.

Viele weitere Einzelheiten zu diesem Thema gibt es auf Fibonacci Numbers, the Golden section and the Golden String.

↑ nach oben

¬ zurück