Die Quadratur des Kreises und andere Probleme

Archimedes (griechische Briefmarke)

Die Quadratur des Kreises
Die Verdopplung des Würfels
Die Dreiteilung des Winkels
Literatur und Links

Wenn man sagt, jemand versucht die "Quadratur des Kreises", meint man, er hat sich etwas Unmögliches vorgenommen. Ursprünglich handelt es sich dabei darum, einen Kreis in ein flächengleiches Quadrat zu verwandeln. Nach Platos Auffassung von Geometrie waren nur Konstruktionen mit Zirkel und Lineal (ohne Markierungen) erlaubt. So versuchten die griechischen Mathematiker, mit diesen Mitteln das Problem zu lösen - allerdings ohne Erfolg. Ähnlich erging es ihnen mit zwei anderen Aufgaben, der "Verdopplung des Würfels" und der "Dreiteilung des Winkels". Erst im 19. Jahrhundert konnte mit den Mitteln der modernen Algebra gezeigt werden, dass keine dieser drei Konstruktionen mit Zirkel und Lineal durchgeführt werden kann.

Ganz anders sieht die Sache aus, wenn man auch andere Hilfsmittel zulässt - ein markiertes Lineal, Kegelschnitte oder spezielle Kurven. Dann gibt es für diese Probleme eine Vielzahl von Lösungen, von denen etliche schon in der Antike entdeckt wurden. Einige davon will ich jetzt vorstellen.

(Die Beweise habe ich allerdings in moderner Schreibweise formuliert, weil die Ausdrucksweise der griechischen Mathematiker für uns sehr ungewohnt ist. Wer will, kann sie auch ganz überspringen.)

Die Quadratur des Kreises

"Quadratur" ist ein alter Ausdruck für "Flächenbestimmung". Euklid hat in Buch I und II der "Elemente" gezeigt, wie man eine beliebige geradlinige Figur in ein Rechteck mit gleichem Flächeninhalt und dieses in ein Quadrat verwandelt (siehe "Mittelwerte": Geometrisches Mittel). Daher lag der Gedanke nahe, dasselbe auch für einen Kreis zu versuchen. Das ist gleichbedeutend damit, eine Strecke zu konstruieren, die gleich lang wie der Kreisumfang ist, bzw. den Wert von p geometrisch zu bestimmen.

Die Quadratrix

Im 4. Jahrhundert v.Chr. fand Deinostratus eine Lösung mit Hilfe der Quadratrix, einer von Hippias entdeckten Kurve. Sie entsteht auf folgende Weise:

Wir gehen aus von einem Quadrat ABCD. Während die Strecke AD um A rotiert, wird die Strecke CD parallel nach unten verschoben, und zwar so, dass beide gleichzeitig den unteren Rand des Quadrats erreichen. Der Schnittpunkt F der beiden Strecken beschreibt dabei eine Kurve, die Quadratrix, die die Seite AB in G trifft.

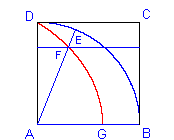Deinostratus konnte nun zeigen:

AG : AB = AB : Kreisbogen BED

Damit kann man eine Strecke konstruieren, die genauso lang ist wie der Viertelkreis.

Beweis: Angenommen, AB = 1. Wir stellen die Gleichung der Kurve in Polarkoordinaten auf.
Aus der Definition der Quadratrix folgt für die Koordinaten von F:

Andrerseits gilt: y = r·sin j, daher erhalten wir
und
Daraus kann man leicht die angegebene Proportion nachrechnen.

Allerdings warfen Deinostratus' Zeitgenossen ihm vor, dass er gemogelt habe. Denn wenn sich ein Punkt entlang der Quadratseite und der andere in derselben Zeit entlang des Kreisbogens bewegen soll, muss man das Verhältnis dieser beiden Größen schon kennen - er setzt also das voraus, was er erst berechnen will.

Archimedes' Beiträge - die archimedische Spirale

Archimedes von Syrakus (287 - 212 v.Chr.) hat sich ausführlich mit der Quadratur des Kreises beschäftigt. In seinem Buch "Die Kreismessung" beweist er, dass der Flächeninhalt eines Kreises genauso groß ist wie der eines Dreiecks, das den Kreisumfang als Basis und den Radius als Höhe hat. Wenn man den Umfang eines Kreises konstruieren kann, kennt man also auch die Fläche. 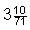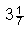Außerdem zeigt er, dass das Verhältnis des Umfangs zum Durchmesser (das, was wir heute mit p bezeichnen) zwischen und liegt - eine Näherung, die jahrhundertelang für alle praktischen Zwecke genügte.

In seinem Werk "Über Spiralen" gibt Archimedes auch eine genaue Konstruktion an. Er definiert eine Spirale so:

"Wenn sich ein Strahl in einer Ebene um seinen Endpunkt mit gleichförmiger Geschwindigkeit dreht, nach einer beliebigen Anzahl von Drehungen wieder in die Anfangslage zurückkehrt und sich auf dem Strahl ein Punkt mit gleichförmiger Geschwindigkeit, vom Endpunkt des Strahls beginnend, bewegt, so beschreibt dieser Punkt eine Spirale."

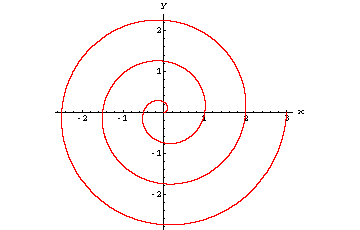
Die Abbildung zeigt die ersten drei Umdrehungen.
In Polarkoordinaten lautet die Gleichung einer solchen Kurve:

r = aj

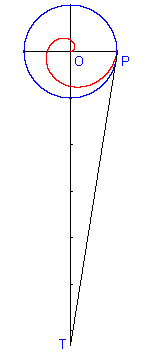Damit kann man folgendermaßen den Umfang eines Kreises konstruieren:

O sei der Mittelpunkt der Spirale, P der Endpunkt der ersten Umdrehung. Wir zeichnen durch O eine Normale zu OP und in P die Tangente an die Spirale. Den Schnittpunkt dieser beiden Geraden nennen wir T. Dann ist OT gleich dem Umfang des Kreises mit dem Radius OP.

Beweis:
Wir bezeichnen die Strecke OP (die "erste Strecke", wie sie Archimedes nennt) mit r₁.
Aus der Gleichung der Spirale folgt: r₁ = 2ap.
Für den Winkel y zwischen der Tangente und dem Radius gilt:

Aus dem Dreieck OPT lesen wir ab:
OT = r₁·tan y = 2pr₁, was zu beweisen war.

Das Dreieck OPT hat also denselben Flächeninhalt wie der Kreis.

Weiter: Die Verdopplung des Würfels